Deltahedron

Not to be confused with Deltohedron.

A deltahedron is a polyhedron whose faces are all equilateral triangles. The deltahedron is named by Martyn Cundy, after the Greek capital letter delta resembling a triangular shape. There are eight convex deltahedra, and they were called convex pseudoregular polyhedra by Rausenberger (1915), who provided the answer to the problem about the number of convex deltahedra that exist. There are infinitely many non-convex deltahedra.

Examples and definitions

One of eight convex deltahedra, the triaugmented triangular prism.

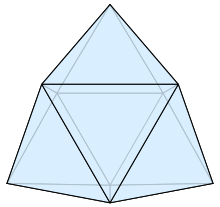
Of the eight convex deltahedra, three are Platonic solids and five are Johnson solids. They are:

• regular tetrahedron, a pyramid with four equilateral triangles, one of which can be considered as the base.
• triangular bipyramid, regular octahedron, and pentagonal bipyramid, a bipyramid with six, eight, and ten equilateral triangles, respectively. They are constructed by identical pyramids base-to-base.
• gyroelongated square bipyramid and regular icosahedron are constructed by attaching two pyramids onto a square antiprism or pentagonal prism, respectively, such that they have sixteen and twenty triangular faces.
• triaugmented triangular prism, constructed by attaching three square pyramids onto the square face of a triangular prism, such that it has fourteen triangular faces.
• snub disphenoid, with twelve triangular faces, constructed by involving two regular hexagons in the following order: these hexagons may form a bipyramid in degeneracy, separating them into two parts along a coinciding diagonal, pressing inward on the end of diagonal, rotating one of them in 90°, and rejoining them together.

The number of possible convex deltahedrons was given by Rausenberg (1915), using the fact that multiplying the number of faces by three results in each edge is shared by two faces, by which substituting this to Euler's polyhedron formula. In addition, it may show that a polyhedron with eighteen equilateral triangles is mathematically possible, although it is impossible to construct it geometrically.

By summarizing the examples above, the deltahedra can be conclusively defined as the class of convex polyhedra whose faces are equilateral triangles. A polyhedron is said to be convex if a line between any two of its vertices lies either within its interior or on its boundary. Additionally, a polyhedron is "strictly" convex if no two faces are coplanar (lying in the same) and no two edges are collinear (segments of the same line). Another definition by Bernal (1964) is similar to the previous one, in which he was interested in the shapes of holes left in irregular close-packed arrangements of spheres. It is stated as a convex polyhedron with equilateral triangular faces that can be formed by the centers of a collection of congruent spheres, whose tangencies represent polyhedron edges, and such that there is no room to pack another sphere inside the cage created by this system of spheres. Because of this restriction, some polyhedrons may be not included as a deltahedron: the triangular bipyramid (as forming two tetrahedral holes rather than a single hole), pentagonal bipyramid (because the spheres for its apexes interpenetrate, so it cannot occur in sphere packings), and regular icosahedron (because it has interior room for another sphere).

A non-convex deltahedron is a deltahedron that does not possess convexity, meaning it has coplanar faces and/or collinear edges. There are infinitely many non-convex deltahedrons. Two examples of such are stella octangula and Boerdijk–Coxeter helix.

Apppearance

Most convex deltahedrons can be found in the study of chemistry. For example, they are categorized as the closo polyhedron. Other application of deltahedrons are the visualization of an atom cluster surrounding a central atom as a polyhedron in the study of chemical compounds.

Some deltahedra appear in solutions of the Thomson problem, concerning the minimum-energy configuration of $n$ charged particles on a sphere.

References

Works cited

• Bernal, J. D. (1964), "The Bakerian Lecture, 1962. The Structure of Liquids", Proceedings of the Royal Society of London, Series A, Mathematical and Physical Sciences, 280 (1382): 299–322, Bibcode:1964RSPSA.280..299B, doi:10.1098/rspa.1964.0147, JSTOR 2415872, S2CID 178710030.
• Boissonnat, J. D.; Yvinec, M. (June 1989), "Probing a scene of non convex polyhedra", Proceedings of the fifth annual symposium on Computational geometry: 237–246, doi:10.1145/73833.73860.
• Caspar, Donald L. D. (1993), Deltahedral views of fullerene polymorphism, doi:10.1098/rsta.1993.0047.
• Cromwell, Peter R. (1997), Polyhedra, Cambridge University Press.
• Cundy, H. Martyn (1952), "Deltahedra", Mathematical Gazette, 36: 263–266, doi:10.2307/3608204, JSTOR 3608204.
• ———; Rollett, A. (1989), "3.11. Deltahedra", Mathematical Models (3rd ed.), Stradbroke, England: Tarquin Pub., pp. 142–144.
• Eppstein, D. (2021), "On Polyhedral Realization with Isosceles Triangles", Graphs and Combinatorics, 37, Springer: 1247–1269, doi:10.1007/s00373-021-02314-9
• Foulds, L. R.; Robinson, D. F. (1979), "Construction properties of combinatorial deltahedra", Discrete Applied Mathematics, 1 (1–2): 75–87, doi:10.1016/0166-218X(79)90015-5.
• Freudenthal, H.; van der Waerden, B. L. (1947), "On an assertion of Euclid", Simon Stevin, 25: 115–121, MR 0021687.
• Gardner, Martin (1992), Fractal Music, Hypercards, and More: Mathematical Recreations from Scientific American, New York: W. H. Freeman, pp. 40, 53, and 58–60.
• Kharas, K. C. C.; Dahl, L. F. (1988), "Ligand-Stabilized Metal Clusters: Structure, Bonding, Fluxionarity, and the Metallic State", in Prigogine, I.; Rice, S. A. (eds.), Evolution of Size Effects in Chemical Dynamics Part 2: Advances in Chemical Physics Volume LXX, John Wiley & Sons, p. 8.
• Litchenberg, D. R. (1988), "Pyramids, Prisms, Antiprisms, and Deltahedra", The Mathematics Teacher, 81 (4): 261–265, JSTOR 27965792
• Pedersen, M. C.; Hyde, S. T. (2018), "Polyhedra and packings from hyperbolic honeycombs", Proceedings of the National Academy of Sciences, 115 (27): 6905–6910, doi:10.1073/pnas.1720307115
• Pugh, Anthony (1976), Polyhedra: A visual approach, California: University of California Press Berkeley, pp. 35–36, ISBN 0-520-03056-7.
• Rausenberger, O. (1915), "Konvexe pseudoreguläre Polyeder", Zeitschrift für mathematischen und naturwissenschaftlichen Unterricht, 46: 135–142.
• Sloane, N. J. A.; Hardin, R. H.; Duff, T. D. S.; Conway, J. H. (1995), "Minimal-energy clusters of hard spheres", Discrete & Computational Geometry, 14 (3): 237–259, doi:10.1007/BF02570704, MR 1344734, S2CID 26955765.
• Smith, James T. (2000), Methods of Geometry, John Wiley & Sons, p. 420
• Trigg, Charles W. (1978), "An Infinite Class of Deltahedra", Mathematics Magazine, doi:10.1080/0025570X.1978.11976675.